Формулы сокращённого умножения для 2 многочленов:

Квадрат суммы:       (a + b)² = a² + 2ab + b²   – Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого выражения на второе, плюс квадрат второго выражения.

Квадрат разности:   (a – b)² = a² – 2ab + b² – Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого выражения на второе, плюс квадрат второго выражения.

Разность квадратов: a² – b² = (a – b)(a + b) – Разность квадратов двух выражений равна произведению их разности и их суммы.

Сумма кубов:     a³ + b³ = (a + b)(a² – ab + b²) – Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат разности.

Разность кубов:  a³ – b³ = (a – b)(a² + ab + b²) – Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат суммы.

Куб суммы:        (a + b)³ = a³ + 3a²b + 3ab² + b³ – Куб суммы двух выражений равен кубу первого выражения, плюс утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение первого выражения и квадрата второго, плюс куб второго выражения.

Куб разности:     (a – b)³ = a³ – 3a²b + 3ab² – b³ – Куб разности двух выражений равен кубу первого выражения, минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение первого выражения и квадрата второго, минус куб второго выражения.

В теории многочленов часто двучлены называют биномами.

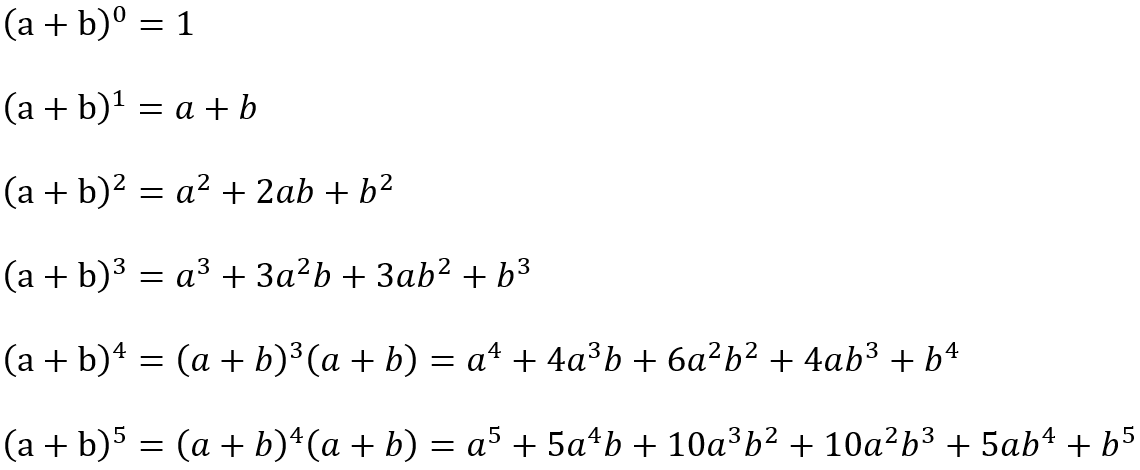
Биноминальная формула Ньютона, Бином Ньютона, Биномиальные коэффициенты, Свойство биномиальных коэффициентов, Треугольник Паскаля